概率复习合集
概率问题的学习/复习整理。
目录:
题目及参考资料出自以下来源:
重要定义
大数定律与中心极限定理
- 大数定律 : 当n足够大时,样本均值和数学期望充分接近,即随机试验的结果频率趋近于概率。
- 中心极限定理 : 当n足够大时,样本均值的分布呈现正态分布,m轮n次实验得出的m次样本均值呈现正态分布。
- 区别 : 大数定律谈论均值,中心极限定理谈论分布。
- 补充:
- 切比雪夫不等式:独立分布数列,方差存在且有共同上界,则符合大数定律。
全概率与贝叶斯
- 全概率 : 知因求果。P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)P(A|B3)+⋯
-
贝叶斯 : 知果求因。P(B1|A) = P(AB1)/P(A) = P(B1)P(A|B1)/P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)P(A|B3)+⋯ 。
其原理是已知某些特征和某些结果的对应关系(如感冒或发烧均会导致打喷嚏对应),当已知结果时倒推由某一特征引起的可能性(在已知打喷嚏的情况下,求是感冒引起打喷嚏的可能性)。前提是特征间各自独立且完备。
- 贝叶斯定理同时还是贝叶斯算法的基础。贝叶斯算法常应用在需要分类、NLP的场景中,可参考:分类算法学习(二)——贝叶斯算法的原理及简单实现
典型问题
最佳停止问题(37法则)
选择策略为:在总共n个备选物体中,跳过前k个物体,从k+1个物体开始,选择第一个比k中最好的备选项中更好的第一个备选项i。
若要使最后选择的备选项i是最优选择,必须满足n个备选项中的次优项出现在前k个物体中。
则当i一定时,P(被选中的i为最优选项)为在k/i-1,即在i-1个位置中选k个位置。
具体解法如下图,最后得出最优策略为跳过前37%。

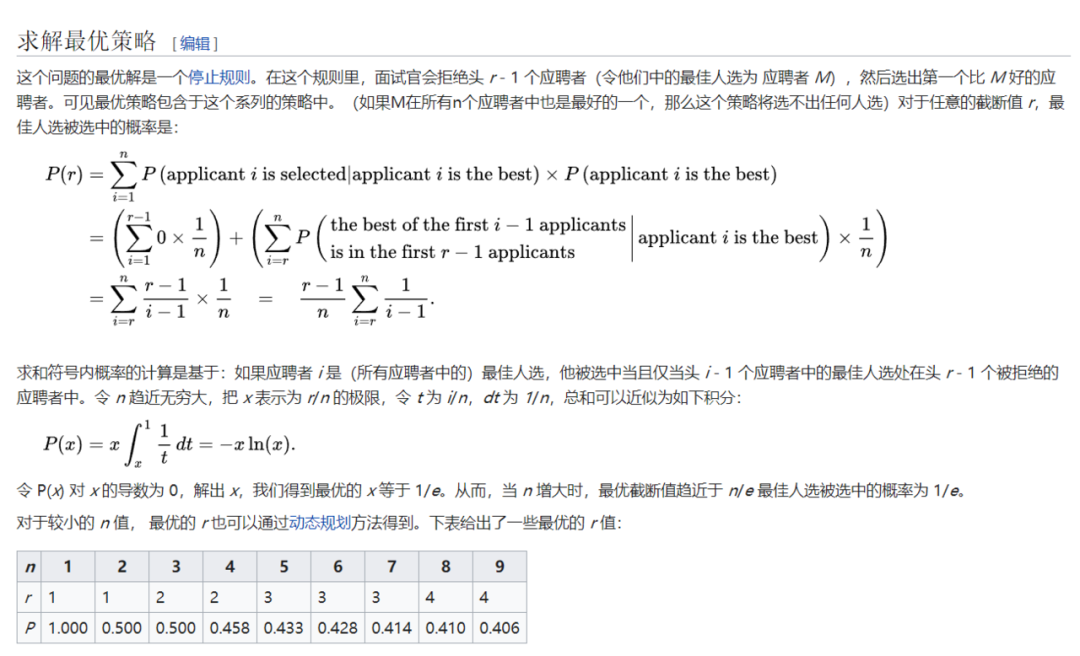
公司最佳员工数
题 :某大公司有这么一个规定:只要有一个员工过生日,当天所有员工全部放假一天。但在其余时候,所有员工都没有假期,必须正常上班。这个公司需要雇用多少员工,才能让公司一年内所有员工的总工作时间期望值最大?
思路 :最大似然估计,已知数据求参数。设员工生日服从均匀分布。公司某一天工作的可能性为 (364/365)^ n,则1天的总工作时间期望为 E = n * (364/365)^ n。求解时两边同取对数求导。
组成三角形的可能性
题 :一根线,随机在A、B两处落剪,问三个线段组成三角形的概率是多少?
思路 :这是一道线性规划问题,约束条件有:
- x, y, a-x-y > 0
- x+y > a-x-y
- a-y > y
- a-x > x
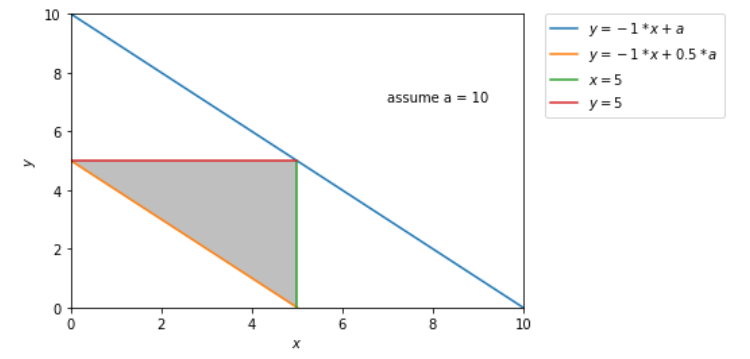
解题 :在pdd面试的时候问到了,可惜我当时太紧张了,只回答了一个大概的思路(捂脸),没有实际算出来。想尝试用Python写出答案,结果发现Python里大多数包需要给定目标函数,以求出线性规划的最优解。
所以最后还是要靠手画,从图上看出阴影面积。用Python作图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import matplotlib.pyplot as plt
import random
# %matplotlib inline
# Construct lines
a = 10 # x's value doesn't matter
x = np.linspace(0.0,10.0,100)
# Make plot
plt.plot(x, -1*x + a, label=r'$y = -1*x + a$') # a-x-y > 0
plt.plot(x, -1*x + 0.5*a, label=r'$y = -1*x + 0.5*a$') # x+y > a-x-y
plt.plot([5]*100, np.linspace(0.0,5.0,100), label=r'$x = 5$') #a-x> x
plt.plot(np.linspace(0.0,5.0,100), [5]*100, label=r'$y = 5$') # a-y > y
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.xlim((0.0, 10.000))
plt.ylim((0.0, 10.000))
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.text(7,7,"assume a = 10")
x1,y1 = (0.5*a, 0)
x2,y2 = (0, 0.5*a)
x3,y3 = (0.5*a, 0.5*a)
plt.fill([x1,x2,x3,x1],[y1,y2,y3,y1],'grey',alpha=0.5)
plt.show()